Travaillant sur un projet de textes fondateurs de la science française (début du XIX° siècle) sur Internet, dans le cadre de science.gouv.fr, j'ai étudié deux pages du mathématicien Joseph Liouville (1809-1882), comptes-rendus de l'Académie des Sciences de mai 1844. Dans ces deux pages, Liouville découvre (au sens d'une véritable découverte) les nombres qui ne sont pas des irrationnels algébriques, et qui prendront plus tard le nom de " nombres transcendants ".
Figure : Avant Liouville, personne n'imaginait qu'il pouvait y avoir d'autres nombres , non algébriques (les nombres algébriques sont solutions d'un polynôme algébrique). Ils appartiennent aux réels R sans être dans les algébriques A: ils correspondent à la zone hachurée de la figure ci-contre.
Liouville commence par établir l'inégalité qui porte son nom.
Pour tout nombre algébrique x solution d'une équation algébrique de degré n>1 (c'est à dire tout nombre algébrique non rationnel), il existe une constante A, tel que pour tout nombre rationnel p/q, on a 
Nous ne l'établirons pas ici (vous pouvez trouver la démonstration sur Wikipedia ; elle utilise le théorème de Rolle décrit dans un post précédent). La subtilité de l'inégalité tient dans la différence entre nombre algébrique irrationnel et nombre rationnel : elle découle du fait que, pour tout rationnel p/q, la valeur qnf(p/q), où f est le polynôme algébrique dont x est une solution, est un entier non nul, donc supérieur à 1 en valeur absolue...entre f(x) et qnf(p/q), il y a au moins 1, donc entre x et p/q il y a au moins quelque chose.
L'inégalité n'est pas très facile à interpréter en raison de la présence de qn au dénominateur: disons, en première approximation, qu'un nombre algébrique non rationnel " ne se laisse pas approcher de trop près par un rationnel ".
Mais Liouville va plus loin, et de manière elliptique, dans la dernière phrase de son article, donne des exemples de nombres non algébriques. Il observe que le nombre :
Est " trop bien approché " par les sommes partielles:
Examinons en effet la quantité:
Le premier 1 y apparaît à la position (N+1)! après la virgule, et d'autres 1 apparaissant après. On peut donc majorer cette quantité par exemple par le nombre où 2 apparaît à la position (N+1)! après la virgule, suivi de 0 après.
On voit aisément que, quel que soit n fixé, pour N grand cette quantité tend vers 0, et peut être rendue inférieure à toute constante A . C'est parce qu'on a pris les puissances factorielles au dénominateur qu'on obtient ce résultat. Ceci contredit l'inégalité de Liouville et permet de conclure que y n'est pas algébrique, donc transcendant. On notera au passage qu'un nombre algébrique irrationnel ne peut être " approché de trop prés " par des nombres rationnels (inégalité de Liouville), en revanche un nombre transcendant peut être ainsi " approché " par des rationnels.
Essayons d'imaginer maintenant ces différents ensembles : Q (rationnels) est dénombrable, A (algébriques) est dénombrable, A et Q ne se " mélangent pas " ; T (transcendants) est non dénombrable, les transcendants (ensemble dense) " s'approchent " de tous les rationnels et algébriques.
Le nombre: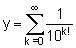
est le premier nombre transcendant connu, égal à 0,110001... , est appelé nombre de Liouville en hommage au " découvreur des nombres transcendants ".
