| Navigation |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
| |
FONCTIONS LOGARITHMES
ET EXPONENTIELLES
I Situation
L’entreprise Lartronic S.A conçoit et commercialise des filtres passifs électroniques (Passe-bas , passe-haut et passe-bande). Ils se présente sous forme de circuits intégrés pouvant contenir de 2 à 4 filtres. Hormis leur catalogue, le client peut demander du "sur mesure" en donnant ses fréquences de coupure.
Il est donc nécessaire pour la conception de maîtriser les fonctions logarithmiques.
Illustration 1 : Filtre passe-bande

Illustration 2 : Modélisation d’un filtre

Illustration 3 : Expression du gain

********************************************
De plus, nous avons vu dans le chapitre sur les complexes, que la notation exponentielle était la plus usité. Nous verrons ultérieurement que dans les mathématiques du traitement du signal elles seront encore présentes (Transformées de Laplace, transformées de Fourier).
II Fonction logarithme népérien
- Définition
On appelle logarithme népérien, noté ln ou Log, la primitive de la fonction  pour x>0 et s’annulant pour x = 1. pour x>0 et s’annulant pour x = 1. 

Remarque épistémologique: Les deux fonctions logarithmes les plus utilisées sont celles à base e = 2,71828…. et à base 10 . On les appelait respectivement autrefois le grand log (Log)et le petit log (log). Aujourd’hui, logarithme népérien (ln) et logarithme à base 10 (log)
- Propriétés
2-a) Propriété fondamentale
  
Démonstration :
Considérons la fonction ln (a.x)
Sa dérivée est  . .
Si on intègre cette égalité on obtient ln(a.x) = lnx + C
En posant x = 1 , et à l’aide de la définition on obtient que lna = C
Et en posant enfin x = b 
2-b) Conséquences





- Etude la fonction y = lnx
- Par construction, la fonction logarithme népérien est définie, continue et dérivable sur

- Sens de variation
 strictement croissante strictement croissante
- Branches infinies
* En l’infini
 et x>1 est toujours comprise entre 2 puissances successives de a : et x>1 est toujours comprise entre 2 puissances successives de a :


comme  alors alors  donc donc 
Recherchons maintenant 

D’après le graphique, il est évident que lnx est inférieur au rectangle (1,x,B,A)
Démonstration :







L’axe Ox est donc Branche Parabolique de Direction Asymptotique .
 Plus généralement, on retiendra Plus généralement, on retiendra  avec avec 
* En zéro
Dans la recherche de  , posons , posons  ce qui nous permet ce qui nous permet
d’écrire :

La courbe possède donc une asymptote verticale en x = 0.
- Le tableau de variations donne donc :

On remarque que pour x = 1 , y = 0 , y’(1) = 1
Pour x= e » 2.71828 , y = 1
La dérivée seconde  nous donne une concavité toujours tournée vers les y négatifs. nous donne une concavité toujours tournée vers les y négatifs.

- A propos de la dérivée et de la primitive
4-a) On remarque que la fonction g(x) = ln(1 + x) est dérivable en zéro, son calcul
nous donne
 . .
Ce qui nous permet d’écrire l’infiniment petit :

4-b) Calculons la dérivée de y = ln|x|
si x>0 Þ y = lnx Þ y’= 
si x<0 Þ y = ln(–x) Þ y’ = 
alors on retiendra  ou encore ou encore  où u(x) est une fonction de x. où u(x) est une fonction de x.
III Fonction logarithme de base a
- Définition
On appelle logarithme de base a, notée  , la fonction définie par , la fonction définie par
  
Regardons la variation de cette courbe en calculant la dérivée 
Donc si   
Et si   
On peut aussi remarquer  
D’ou les courbes

- Changement de base
Il est très utile de passer d’un logarithme à une base a donnée à un logarithme d’une autre base b par exemple. Le cas le plus connu pour les scientifiques étant le passage du logarithme népérien au logarithme de base 10 ( noté maintenant log x) dont la réciproque, que nous définirons après, est noté maintenant log x) dont la réciproque, que nous définirons après, est  utilisée dans tous les domaines de la physique et de la chimie. utilisée dans tous les domaines de la physique et de la chimie.
Soit donc b une nouvelle base.

D’où la formule du changement de base

Cas particulier à retenir : a = e et b = 10 
D’où  et inversement et inversement 
IV Fonction exponentielle
- Définitions
Les fonctions  sont continues et monotones pour x>0. Elles réalisent de ce fait une bijection de R*+ sur R et sont donc inversibles. Leurs fonctions réciproques sont appelées exponentielles de base a et notée expa et sont définies sont continues et monotones pour x>0. Elles réalisent de ce fait une bijection de R*+ sur R et sont donc inversibles. Leurs fonctions réciproques sont appelées exponentielles de base a et notée expa et sont définies
par  ou ou 
Ces fonctions sont continues et monotones pour tout x et établissent une bijection de R sur R*+ avec  
Les points particuliers sont définis par :


On notera les deux fonctions exponentielles essentielles
 et et 
- Propriétés
2-a) Relation fondamentale
  
entraîne 
ou 
2-b) limites comparées
 Nous avons vu précédemment que " Puissance l’emporte sur logarithme ", on retiendra de la même façon que " exponentielle l’emporte sur puissance " Nous avons vu précédemment que " Puissance l’emporte sur logarithme ", on retiendra de la même façon que " exponentielle l’emporte sur puissance "
 avec avec 
V Fonctions exponentielles généralisées
Ce sont des fonctions dont la présentation est de la même forme qu’une exponentielle ou une fonction puissance, mais où u(x) et v(x) sont des fonctions de x.

Il est cependant impossible d’étudier ces fonctions telles qu’elles se présentent. Il faut revenir à une notation exponentielle classique.
 
On retiendra cette dernière expression.
VI Echelle logarithmique
Lorsqu’on étudie un phénomène représenté par une fonction f(x) sur une gamme étendue de valeurs de x, l’échelle linéaire pour les abscisses est mal adaptée. On lui préfère une échelle logarithmique, en général de base 10. Elle permet de " dilatée " les faibles et les fortes valeurs.
En appelant a la distance entre les extrémité d’une décade (dizaine), on place x sur l’échelle logarithmique à l’aide de son représentant a .log x . Ce qui nous donne :

I. Puissance d'un réel strictement positif
Pour tout x > 0 et pour tout 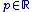 on a : on a :
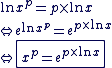
Définition : Soit 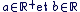
On appelle ab le nombre réel défini par 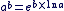
Propriétés : Pour tout réel a strictement positif et pour tous les réels b et c, on a :

Démonstration :
II-La fonction racine enieme
Théorème - Définition :
Soient n un entier naturel non nul et a un réel strictement positif.
L'équation xn = a admet une unique solution dans 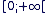 appelée racine énième de a. Elle est notée appelée racine énième de a. Elle est notée 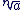
Démonstration :
Etudions sur 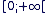 la fonction f : x la fonction f : x  xn xn
f'(x) = n × xn-1
Sur l'intervalle considéré, 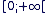 , on a f'(x) > 0, , on a f'(x) > 0,
donc f est strictement croissante sur 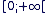 et elle est de plus continue sur cet intervalle. et elle est de plus continue sur cet intervalle.
D'autre part on a :
f(0) = 0n et 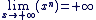
L'intervalle image est donc 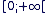 (identique à l'intervalle de définition). (identique à l'intervalle de définition).
Sur 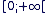 la fonction est donc dérivable, continue et strictement croissante : pour tout la fonction est donc dérivable, continue et strictement croissante : pour tout 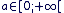 il existe une unique valeur de x telle que xn = a il existe une unique valeur de x telle que xn = a
Remarque :
1. Pour tout x appartenant à 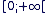 , xn = 0 admet une unique solution : , xn = 0 admet une unique solution : 
2. xn = a avec a > 0 et x > 0
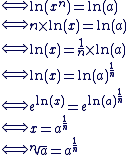
Propriétés :
Si a > 0, alors 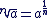
Si a = 0, alors 
Donc, pour tout 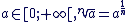
Définition :
On appelle fonction racine énième la fonction définie sur 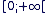 par par 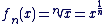
Etude de la fonction :
Sur 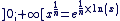
Ici le problème mis en évidence vient de l'écriture logarithmique : on ne peut l'utiliser que si x > 0, donc 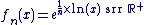
Dérivée :
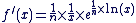
Sur 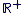

Donc f'(x) est strictement positive sur 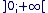 et f est strictement croissante sur cet intervalle. et f est strictement croissante sur cet intervalle.
Limite :
En 0+ :
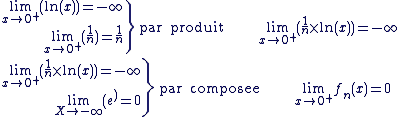
En 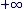

Continuité en 0 :
On a : 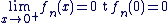
Donc fn est continue en 0.
Dérivabilité en 0 :
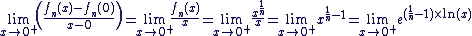
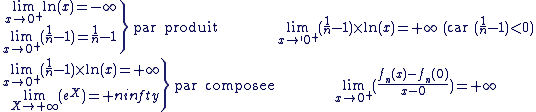
La fonction n'est pas dérivable en 0 et la courbe admet une demi-tangente verticale en ce point.
On a donc :
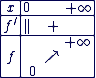
La comparaison des croissances respectives des fonctions ex, xn et ln x peuvent permettre de lever certaines indéterminations se présentant lors du calcul des limites de fonctions.
Nous avons (pour n  *) : *) :
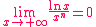
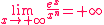
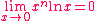
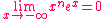
Exemple d'application 1
Calculer 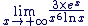
 Nous allons nous ramener à une formule du cours : Nous allons nous ramener à une formule du cours :
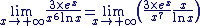
 Appliquons les théorèmes de croissance comparée : Appliquons les théorèmes de croissance comparée :
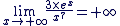 et et 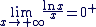
donc 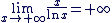
 Conclusion : Conclusion :
Nous avons donc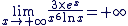
Exemple d'application 2
Démontrer que 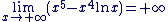
 Nous pouvons nous ramener à une formule du cours, afin d'appliquer les théorèmes de croissance comparée. Nous pouvons nous ramener à une formule du cours, afin d'appliquer les théorèmes de croissance comparée.
Pour cela, mettons en facteur le terme dominant :
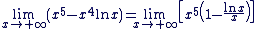
Nous savons que 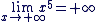 . .
Et que 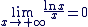 d'où d'où 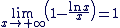
 Conclusion : Conclusion :
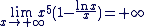 . .
On a bien : 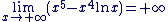
Exemple d'application 3
Déterminer 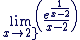
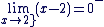 donc donc 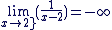
Posons 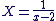 . Ce changement de variable nous permet d'utiliser le fait que : . Ce changement de variable nous permet d'utiliser le fait que :
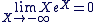 pour déduire que : pour déduire que :
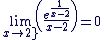
Résolution avec second membre
position du probléme
L'énoncé introduit une équation différentielle avec second membre ( par exemple 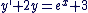 ) et pose des questions destinées à la résoudre. ) et pose des questions destinées à la résoudre.
Ces questions sont pratiquement toujours les mêmes, mais n'ont pas forcément le même ordre que celui donné dans le principe suivant.
Principe :
Pour résoudre l'équation avec second membre (E) on demande de :
a) Résoudre l'équation sans second membre(E')
b) Montrer qu'une fonction g est solution de (E)
c) Montrer que f est solution de (E) si et seulement si (f-g) est solution de (E')
d) En déduire les solutions de (E)
Exercice concret
Résolution de 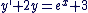 (E) (E)
a) résoudre y'+2y=0 (E')
b) Déterminez a et b de façon à ce que g définie sur 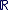 par par 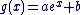 soit solution de (E) soit solution de (E)
c) Montrez que f est solution de (E) si et seulement si (f-g) est solution de (E ')
d) Déduisez-en les solution s de (E)
a) On applique la propriété du cour , on trouve que les solutions de (E ') sont les fonctions 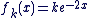
b) Le principe de ce genre de question est de remplacer y par g et d'identifier alors les constantes . allons-y :
g est dérivable sur 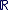 et et 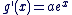
on en déduit que 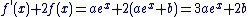
f sera donc solution de (E) si 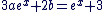 c'est-à-dire si a et b vérifient : c'est-à-dire si a et b vérifient :
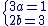
c'est-à-dire pour 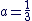 et et 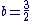
On a donc : 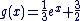
c) f-g est solution de (E') :
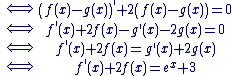
(on a 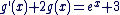 car g est solution de l'équation avec second membre) car g est solution de l'équation avec second membre)
 f solution de (E) f solution de (E)
REMARQUE :
Retenez bien ces différentes phases car c'est toujours pareil. L'important étant de partir de (f-g) et de faire dérouler la démonstration.
d) f solution de (E)
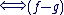 solution de (E') solution de (E')
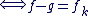 d'après a) d'après a)
 est définie par est définie par 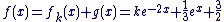
Théorème 1 : Solution générale de l'équation différentielle
L'ensemble des solutions de l'équation différentielle 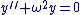 , où , où  est un réel donné, est l'ensemble des fonctions définies sur est un réel donné, est l'ensemble des fonctions définies sur 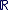 par : par :  , où A et B sont deux constantes réelles quelconques. , où A et B sont deux constantes réelles quelconques.
Exemple :
voir l'exercice 1 ci-dessous. Théorème 2 : Solution vérifiant des conditions initiales
L'équation différentielle 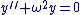 , où , où  est un réel donné, admet une solution unique f, définie sur est un réel donné, admet une solution unique f, définie sur 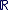 , vérifiant les conditions initiales : , vérifiant les conditions initiales : 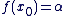 et et 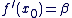
I. Equations du type y' = ky
 Soit k un nombre réel, résoudre l'équation différentielle : y' = ky Soit k un nombre réel, résoudre l'équation différentielle : y' = ky
consiste à déterminer toutes les fonctions f dérivables sur  telles que, pour tout nombre réel x, f'(x) = k f(x). telles que, pour tout nombre réel x, f'(x) = k f(x).
 Les solutions de l'équation différentielle y' = ky sont les fonctions f définies sur Les solutions de l'équation différentielle y' = ky sont les fonctions f définies sur  par : par :
f(x) = C ekx, où c  . .
 Pour tout couple (x0 ; y0) Pour tout couple (x0 ; y0)   ², l'équation y' = ky admet une solution f et une seule telle que f(x0) = y0. ², l'équation y' = ky admet une solution f et une seule telle que f(x0) = y0.
Exemple :
II. Equations du type y' = ay + b
 Soit a et b deux nombres réels, résoudre l'équation différentielle : y' = ay + b Soit a et b deux nombres réels, résoudre l'équation différentielle : y' = ay + b
consiste à déterminer toutes les fonctions f dérivables sur  telles que, pour tout nombre réel x, f'(x) = a f(x) + b. telles que, pour tout nombre réel x, f'(x) = a f(x) + b.
 Les solutions de l'équation différentielle y' = ay + b, avec a Les solutions de l'équation différentielle y' = ay + b, avec a 0, sont les fonctions f définies sur 0, sont les fonctions f définies sur  par : par :
f(x) = C eax - b/a, où c  . .
 Pour tout couple (x0 ; y0) Pour tout couple (x0 ; y0)   ², l'équation y' = ay + b, avec a ², l'équation y' = ay + b, avec a 0, admet une solution f et une seule telle que f(x0) = y0. 0, admet une solution f et une seule telle que f(x0) = y0.
Exemple :
I. Présentation de 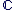
Définition :
L'ensemble 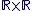 muni des lois de composition internes : muni des lois de composition internes :
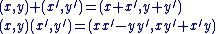
est un corps appelé corps des nombres complexes et noté 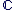 . .
Remarque :
Dans 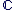 , on définit : , on définit :
 Le zéro : Le zéro : 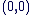 . .
 L'unité : L'unité : 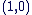 . .
Définition : " L'unité imaginaire d'Euler " :
L'élément 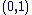 qui vérifie : qui vérifie : 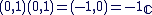 est appelé l'unité imaginaire d'Euler. est appelé l'unité imaginaire d'Euler.
On notera dorénavant 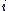 à la place de à la place de 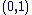 . .
On a : 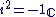 . .
Opposé et inverse d'un élément
 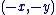 est l'opposé de est l'opposé de 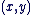 . .
 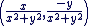 est l'inverse de est l'inverse de  . .
Injection canonique de 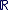 dans dans 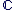
- L'application
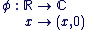 est un morphisme injectif de corps. est un morphisme injectif de corps.
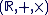 est isomorphe au sous-corps est isomorphe au sous-corps 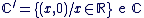 . .- On convient alors d'identifier un élément
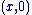 de de 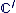 à l'élément à l'élément  de de 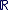 . On écrira donc . On écrira donc  au lieu de au lieu de 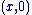 . En particulier : . En particulier :
 à la place de à la place de 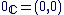 . .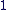 à la place de à la place de 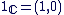 . .
- D'après ce qui précède, on convient de dire que
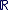 est inclus dans est inclus dans 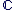 et on note : et on note : 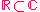 . .
Il est important de noter que l'identification de 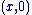 avec avec  n'a de sens que parce qu'il existe l'injection n'a de sens que parce qu'il existe l'injection  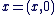 ", l'injection ", l'injection  est sous-entendue, l'écriture correcte étant est sous-entendue, l'écriture correcte étant 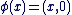 . On dit aussi de manière abusive que . On dit aussi de manière abusive que 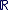 est une partie de est une partie de 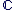 et on note et on note 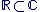 , là encore, l'injection , là encore, l'injection  est sous-entendue. Nous devrions écrire est sous-entendue. Nous devrions écrire 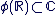 et dire " on identifie et dire " on identifie 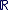 à une partie de à une partie de 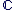 via l'injection canonique via l'injection canonique  ", mais par habitude (système international), on conserve toujours les notations normales (sans noter le ", mais par habitude (système international), on conserve toujours les notations normales (sans noter le  à chaque fois). à chaque fois).
Forme algébrique d'un nombre complexe
Soit 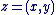 un élément de un élément de 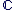 . définie ci-dessus. Ainsi, lorsque l'on écrit " . définie ci-dessus. Ainsi, lorsque l'on écrit "
- Nous adoptons la notation
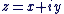 appelée forme algébrique plutôt que la notation appelée forme algébrique plutôt que la notation 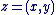 , et nous parlerons de nombre complexe , et nous parlerons de nombre complexe  (ou du complexe (ou du complexe  ) plutôt du couple ) plutôt du couple  . .
- Le réel
 est appelé partie réelle du complexe est appelé partie réelle du complexe  et il est noté et il est noté 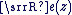 . .
- Le réel
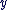 est appelé partie imaginaire du complexe est appelé partie imaginaire du complexe  et il est noté et il est noté 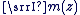 . On a alors : . On a alors : 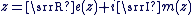 . .
- Deux nombres complexes sont égaux s'ils ont même partie réelle et même partie imaginaire :
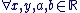 : les deux complexes : les deux complexes 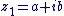 et et 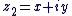 sont égaux ssi : sont égaux ssi :  et et  . .
- Le complexe
 est dit imaginaire pur lorsque : est dit imaginaire pur lorsque : 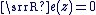 . .
II. Conjugué d'un nombre complexe
Défintion :
Soit 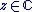 avec avec 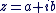 , , 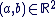 . .
On appelle conjugué du nombre complexe  le nombre complexe noté le nombre complexe noté 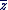 et donné par : et donné par : 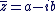 . .
Remarques :
 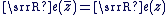 . .
 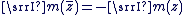 . .
Propriétés :
Pour  et et 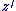 dans dans 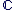 , on a : , on a :
III. Module
Définition :
Soit 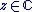 avec avec 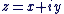 , , 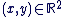 . Le nombre . Le nombre 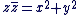 est réel positif. est réel positif.
Le module de  noté noté 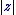 est un réel positif est un réel positif 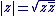 . .
Propriétés :
Pour tout complexe  . .
Propriétés :
Pour tous nombres complexes  et et 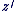 : :
IV. Argument d'un complexe
Introduction :
Soit 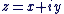 un nombre complexe non nul, avec un nombre complexe non nul, avec  et et 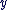 réels. On a : réels. On a :
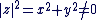 . . 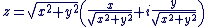 . .
Ou encore, 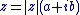 avec avec 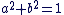 . Cela conduit naturellement à la définition suivante : . Cela conduit naturellement à la définition suivante :
Définition :
Soit 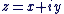 un complexe non nul, avec un complexe non nul, avec  et et 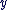 réels. On appelle argument de réels. On appelle argument de  et on note et on note 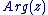 , tout réel vérifiant : , tout réel vérifiant :
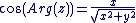 et et 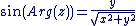 . .
Parmi ces réels (il y en a une infinité), un seul appartient à l'intervalle 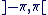 . On l'appelle l'argument principal. Si on le note . On l'appelle l'argument principal. Si on le note  , alors tout argument de , alors tout argument de  vérifie : vérifie :
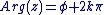 avec avec 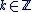 . .
Ce que l'on note :  , et on dit alors que , et on dit alors que 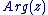 est équivalent (ou congru) à est équivalent (ou congru) à  modulo modulo 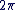 . .
Remarques :
 Contrairement au module qui est défini pour n'importe quel nombre complexe (nul ou non nul), l'argumentnul n'est pas défini. Contrairement au module qui est défini pour n'importe quel nombre complexe (nul ou non nul), l'argumentnul n'est pas défini.
 On retiendra les arguments suivants : On retiendra les arguments suivants :
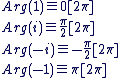
Forme trigonométrique d'un complexe :
D'après ce qui précède, on constate qu'on peut écrire tout complexe  non nul d'argument non nul d'argument 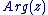 sous la forme suivante appelée forme trigonométrique : sous la forme suivante appelée forme trigonométrique :
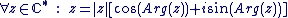 du nombre complexe du nombre complexe
Proposition :
Soit  et et 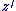 deux complexes non nuls : deux complexes non nuls :
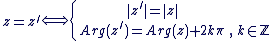
Propriétés :
Soit  un complexe non nul : un complexe non nul :
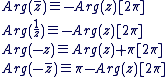
Propriétés :
Soient  et et 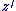 deux complexes non nuls : deux complexes non nuls :
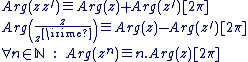
Remarque :
Pour se rappeler de ces trois dernières propriétés de "Arg", il suffit de remarquer qu'elles sont identiques à celles de "ln".
V. Notation exponentielle complexe
Notation :
Il est pratique d'utiliser pour tout 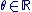 la notation exponentielle complexe la notation exponentielle complexe 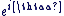 tel que : tel que :
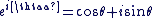
Donc tout complexe  non nul peut s'écrire sous la forme suivante : non nul peut s'écrire sous la forme suivante : 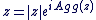 avec avec 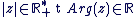
Formules d'Euler :
Pour tout 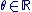 , on a les formules d'Euler suivantes : , on a les formules d'Euler suivantes :

Formule de Moivre :
Pour tout entier relatif  et pour tout et pour tout 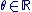 on a : on a :
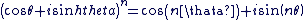
On peut aussi exprimer cette formule en notation exponentielle : 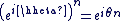
Remarque :
Ces formules précédentes permettent de linéariser des expressions trigonométriques.
Proposition :
 Pour tout Pour tout 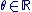 : :
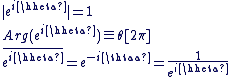
 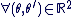 : :
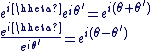
VI. Représentation géométrique
Théorèmes - Définitions :
Soit le plan complexe 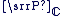 muni d'un repère orthonormal muni d'un repère orthonormal 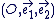 direct et soit direct et soit 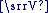 l'ensemble des vecteurs du plan l'ensemble des vecteurs du plan 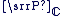 rapporté à le base rapporté à le base 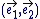 . .
L'application qui, au vecteur 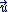 de coordonnées de coordonnées 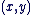 , associe le nombre complexe , associe le nombre complexe 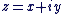 est une bijection de est une bijection de 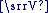 sur sur 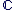 . .
Un argument de  est une mesure de l'angle de vecteurs est une mesure de l'angle de vecteurs 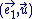 , et , et 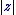 est la norme du vecteur est la norme du vecteur 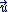 . .
On dit que  est l'affixe de est l'affixe de 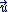 et on note : et on note : 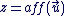 . .
L'application de 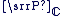 dans dans 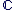 qui, au point qui, au point  de coordonnées de coordonnées 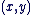 , associe le complexe , associe le complexe 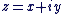 est une bijection de est une bijection de 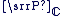 sur sur 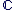 . .
Un argument de  est une mesure de l'angle de vecteurs est une mesure de l'angle de vecteurs 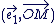 et et 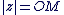 (distance). On dit que (distance). On dit que   et que et que  est l'affixe de est l'affixe de  et on note et on note 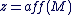 . .
Nombres complexes et transformation
- Translation
Soit b un nombre complexe fixé, f l'application qui à tout point M d'affixe z associe le point M' d'affixe z' = z + b.
est la translation de vecteur  d'affixe b. d'affixe b.

Pour comprendre : on a z' - z qui l'affixe du vecteur 
et b qui est l'affixe d'un vecteur  donc donc  = =  ce qui correspond bien à la définition de M a pour image M' par la translation de vecteur ce qui correspond bien à la définition de M a pour image M' par la translation de vecteur 
- Rotation de centre O
Soit a un nombre réel fixé, f l'application qui à tout point M d'affixe z associe le point M' d'affixe z' tel que z' = z eia est la rotation de centre O l'origine du repère et d'angle a.

Pour comprendre : on a z'/z = eia , donc |z'|/|z| = 1 donc OM' = OM
de plus : Arg(z'/z) = a donc ( ; ;  ' ) = a , ce qui correspond bien à la définition de la rotation de centre O. ' ) = a , ce qui correspond bien à la définition de la rotation de centre O.
Exercice interactif
- Rotation de centre
 ( ( ) )
Soit a un nombre réel fixé, l'application f qui à tout point M d'affixe z associe le point M' d'affixe z' tel que z' -  = (z - = (z -  )eia. )eia.
est la rotation de centre  ( ( ) et d'angle a . ) et d'angle a .
De façon plus générale, si a est un nombre complexe de module 1 et différent de 1 et b est un nombre complexe quelconque, l'application qui à tout point M d'affixe z associe le point M' d'affixe z' = az + b est une rotation de centre le point  ( ( ) tel que ) tel que
 = a = a + b. + b.
- Homothétie de centre O et de rapport k
Soit k un réel non nul, et l'application f qui à tout point M d'affixe z associe le point M' d'affixe z' tel que z' = kz est l'homothétie de centre O et de rapport k.
Pour comprendre : on a z' = kz or z' est l'affixe du vecteur  et z' l'affixe du vecteur et z' l'affixe du vecteur  ' donc on a : ' donc on a :  ' = k ' = k  , ce qui correspond bien à la définition d'homothétie de centre O. , ce qui correspond bien à la définition d'homothétie de centre O.
- Homothétie de centre
 ( ( ) et de rapport k ) et de rapport k
Soit k un réel non nul, et  un nombre complexe, l'application f qui à tout point M d'affixe z associe le point M' d'affixe z' tel que un nombre complexe, l'application f qui à tout point M d'affixe z associe le point M' d'affixe z' tel que
z'-  = k(z - = k(z -  ) est l'homothétie de centre ) est l'homothétie de centre  ( ( ) et de rapport k. ) et de rapport k.
Pour comprendre : on a z'-  = k(z - = k(z -  ) or z'- ) or z'-  est l'affixe du vecteur est l'affixe du vecteur  et z - et z -  l'affixe du vecteur l'affixe du vecteur  ' donc on a : ' donc on a :
 ' = k ' = k  , ce qui correspond bien à la définition d'homothétie de centre , ce qui correspond bien à la définition d'homothétie de centre  . .
De façon plus générale, si a est un nombre réel différent de 1 et b est un nombre complexe quelconque, l'application qui à tout point M d'affixe z associe le point M' d'affixe z' = az + b est une homothétie de centre le point  ( ( ) )
tel que  = a = a + b. + b.
- Similitude directe de centre
 ( ( ) de rapport k et d'angle a ) de rapport k et d'angle a
Soit k un réel positif,  un nombre complexe et a un réel, l'application f qui à tout point M d'affixe z associe le point M' d'affixe z' un nombre complexe et a un réel, l'application f qui à tout point M d'affixe z associe le point M' d'affixe z'
tel que z'-  = keia (z - = keia (z -  ) est la similitude directe ) est la similitude directe
de centre  ( ( ), de rapport k et d'angle de mesure a. ), de rapport k et d'angle de mesure a.
( il suffit d'utiliser la composée d'une rotation et d'une homothétie de même centre )
De façon plus générale, si a est un nombre complexe non nul l'application qui à tout point M d'affixe z associe le point M' d'affixe
z' = az + b est une similitude directe de centre le point  ( ( ) tel que ) tel que
 = a = a + b de rapport |a| et d'angle a = Arg(a). + b de rapport |a| et d'angle a = Arg(a).
Exemples
- Symétrie orthogonale d'axe, l'axe des réels :
L'application qui à tout point M du plan d'affixe z associe le point M' d'affixe
z' =  est la symétrie orthogonale d'axe l'axe des réels. est la symétrie orthogonale d'axe l'axe des réels.
-
| Intégrale d'une fonction dérivable |
Définition et propriété :
Soit f une fonction dérivable sur un intervalle I de  , F une quelconque de ses primitives sur I, a et b deux nombres appartenant à I. , F une quelconque de ses primitives sur I, a et b deux nombres appartenant à I.
On appelle intégrale de f entre a et b que l'on note

le nombre réel F(b) - F(a), indépendant du choix de la primitive F.
|
Exemple de calcul d'intégrale :
 |
Intégration par parties
Dans certain cas il est difficile de calculer une intégrale, car on ne connait pas de primitive pour la fonction concernée, c'est dans ce cas que l'on utilise la méthode d'intégration par parties.
Cette méthode consiste à "transporter" le calcul d'une primitive sur une autre fonction.
Soient u et v deux fonctions 2 fois dérivables sur un intervalle I ( condition suffisante ) .
Pour tout couple (a ; b) d'éléments de I on a :

Démonstration :
La fonction uv est une primitive de la fonction
u'v + uv' ( qui est dérivable, donc admet une primitive ) on a donc :

d'où le résultat en utilisant la linéarité de l'intégrale.
Exemple : on veut calculer l'intégrale

on pose :

ce qui permet de calculer l'intégrale :

on dit que l'on a fait une intégration par partie pour calculer cette intégrale.
| Propriétés de l'intégrale |
Dans tout ce qui suit :
- f et g deux fonctions dérivables sur un intervalle I
- a, b, c trois nombres réels de I
- l un nombre réel quelconque
|
propriété de linéarité de l'intégrale
 |
relation de Chasles :
 |
Ordre des bornes :
 |
Positivité de l'intégrale :
si a < b et pour tout réel x de [a ; b] f(x)  0 alors 0 alors
 |
Intégrale et ordre :
si a < b et pour tout réel x de [a ; b] f(x)  g(x) alors g(x) alors
 |
Valeur moyenne de la fonction f sur l'intervalle [a ; b] :
Le nombre m défini par

est appelé valeur moyenne de la fonction f sur l'intervalle [a ; b]. |
 |
| intégrale |
 |
On veut déterminer la valeur approchée de l'intégrale  où f est la fonction définie sur I= [a ; b] pour cela on va partager l'intervalle I en n intervalles égaux de même largeur (b - a)/n : où f est la fonction définie sur I= [a ; b] pour cela on va partager l'intervalle I en n intervalles égaux de même largeur (b - a)/n :

On a :

La méthode des trapèzes consiste à remplacer ces n intégrales par la somme suivante : ( correspondant à la somme des aires algébriques des trapèzes de hauteur ( xi+1 - xi ) et de bases
f(xi+1) et f(xi) :

(où RI et RS sont les valeurs approchées de l'intégrale avec respectivement les méthodes des rectangles supérieure et inférieure )
|
Primitives utilisant des formes composées
Fonction puissance de base a Soit a un nombre réel qui n'est pas un entier relatif ( sinon on se ramène à des fonctions déja connu qui peuvent être définie sur  ou ou  ) , on appelle fonction puissance de base a la fonction qui à tout réel x strictement positif associe le réel ealnx que l'on note aussi xa . ) , on appelle fonction puissance de base a la fonction qui à tout réel x strictement positif associe le réel ealnx que l'on note aussi xa .
Fonction dérivée de cette fonction :

Le signe de la dérivée dépend de a si a > 0 la fonction puissance est croissante sinon elle décroissante.
| Equations différentielles |
| Introduction :
Soit la fonction f définie sur  par f(x) = cos 2x . Cette fonction est dérivable et sa dérivée la fonction f ' est telle que f '(x) = - 2 sin 2x pour réel x par f(x) = cos 2x . Cette fonction est dérivable et sa dérivée la fonction f ' est telle que f '(x) = - 2 sin 2x pour réel x
La fonction f ' est elle même dérivable et sa fonction sa dérivée f'' est telle que f ''(x) = - 4 cos 2x pour tout réel x.
|
on a donc pour tout réel x :
- f(x) = cos 2x
- f '(x) = - 2 sin 2x
- f''(x) = - 4 cos 2x
|
| On peut remarquer que : 4 f(x) + f ''(x) = 0 pour tout réel x.
On dit que l'équation 4 f(x) + f ''(x) = 0 est une équation différentielle , et la fonction f définie sur  par f(x) = cos 2x en est la solution ( on dit aussi fonction intégrale ) . par f(x) = cos 2x en est la solution ( on dit aussi fonction intégrale ) .
Généralement, on écrit plutôt 4y(x) + y''(x) = 0
et de façon plus simple 4y + y'' = 0
|
Remarque :
- Résoudre ( on dit aussi intégrer ) une équation différentielle sur un intervalle I c'est trouver toutes les solutions, sur I de cette équation, c'est à dire toutes les fonctions f qui vérifient l'égalité. L'inconnue de ce type d'équation n'est plus un nombre réel, mais une fonction.
- La courbe représentative d'une fonction f solution est appelée courbe intégrale.
- Si une équation différentielle ne fait intervenir que x, y ,y' ( avec y fonction de x et y' sa dérivée ) on dit que l'équation différentielle est du premier ordre.
- Si une équation différentielle ne fait intervenir que x, y ,y',y'' ( avec y fonction de x et y' sa dérivée , y'' sa dérivée seconde ) on dit que l'équation différentielle est du second ordre.
|
Probabilité Vocabulaire des probabilités :
L'exemple choisi pour introduire le vocabulaire probabiliste est le jet d'un dé )
Epreuve ou expérience aléatoire :
expérience pouvant être répétée dans des conditions identiques et dont l'issue n'est pas prévisible à priori. ( Le jet d'un dé en regardant le nombre correspondant sur la face supérieure est une expérience aléatoire ou une épreuve )
Eventualité , cas possible :
résultat d'une épreuve, notée généralement  1, 1,  2, .... 2, ....
(Exemple : 1,2,3,4,5,6 sont les éventualités de l'expérience aléatoire définie ci-dessus comme exemple )
Univers :
associé à une expérience aléatoire , ensemble des cas possibles d'une expérience aléatoire. L'univers est généralement noté  . .
( exemple choisi  = {1,2,3,4,5,6} ) = {1,2,3,4,5,6} )
Événement :
partie de l'univers.
( Exemple : "obtenir un nombre pair" est un événement, A = {2,4,6} )
- Si une éventualité appartient à un événement, on dit qu'elle réalise cette événement.
- L'événement particulier
 est un événement particulier puisqu'il contient toute les éventualités d'une même expérience aléatoire , il est donc toujours réalisé on l'appelle événement certain. est un événement particulier puisqu'il contient toute les éventualités d'une même expérience aléatoire , il est donc toujours réalisé on l'appelle événement certain.
- Aucune éventualité appartient à l'événement
 , il est donc jamais réalisé, , il est donc jamais réalisé,  est appelé événement impossible. est appelé événement impossible.
Événement élémentaire :
événement réduit à une seule éventualité ( Exemple : "obtenir 6" est un événement élémentaire , B= {6} ) Les événements étant des ensembles on peut définir les mêmes opérations que sur les ensembles.
Si A et B sont deux événements d'une même expérience aléatoire :
- A le complémentaire de A est appelé événement contraire de A. ( Exemple si A est l'événement : A :"Obtenir un nombre pair " , A= {2,4,6} , A est l'événement contraire A: " Ne pas obtenir de nombre pair " , A= {1,3,5} ). Remarque deux événement contraire sont incompatibles.
- A
 B : l'événement A B : l'événement A  B est la réunion des événement A et B . ( Exemple si A est l'événement : A :"Obtenir un nombre pair " , A= {2,4,6} , et B: " Obtenir un nombre supérieur ou égal à 4 ", B={4,5,6} A B est la réunion des événement A et B . ( Exemple si A est l'événement : A :"Obtenir un nombre pair " , A= {2,4,6} , et B: " Obtenir un nombre supérieur ou égal à 4 ", B={4,5,6} A  B : "Obtenir un nombre pair ou B : "Obtenir un nombre pair ou  4" et A 4" et A  B = {2,4,5,6}) B = {2,4,5,6})
- A
 B : l'événement A B : l'événement A  B est l'intersection des événement A et B . ( Exemple si A est l'événement : A :"Obtenir un nombre pair " , A= {2,4,6} , et B: " Obtenir un nombre supérieur ou égal à 4 ", B={4,5,6} A B est l'intersection des événement A et B . ( Exemple si A est l'événement : A :"Obtenir un nombre pair " , A= {2,4,6} , et B: " Obtenir un nombre supérieur ou égal à 4 ", B={4,5,6} A  B : "Obtenir un nombre pair et B : "Obtenir un nombre pair et  4" et A 4" et A  B = {4,6}) B = {4,6})
- Si A
 B = B =  , les événements A et B sont dit incompatibles , il ne peuvent pas se réaliser en même temps ( Exemple si A est l'événement : A :"Obtenir un nombre < 3 " , A= {1,2} , et B: " Obtenir un nombre supérieur ou égal à 4 ", B={4,5,6} A , les événements A et B sont dit incompatibles , il ne peuvent pas se réaliser en même temps ( Exemple si A est l'événement : A :"Obtenir un nombre < 3 " , A= {1,2} , et B: " Obtenir un nombre supérieur ou égal à 4 ", B={4,5,6} A  B : "Obtenir un nombre < 3 et B : "Obtenir un nombre < 3 et  4" et A 4" et A  B = B =  ). ).
Variables aléatoires
Définitions :
On considère une expérience aléatoire d'univers associé  ( fini ou infini ), on appelle variable aléatoire X toute fonction de ( fini ou infini ), on appelle variable aléatoire X toute fonction de  à valeur dans à valeur dans  . .
L'ensemble des images des éléments de  par la variable aléatoire X est appelée univers image, on le note X( par la variable aléatoire X est appelée univers image, on le note X( ) . ) .
Si X( ) est un ensemble fini ou dénombrable, on dit que la variable aléatoire X est discréte, si X( ) est un ensemble fini ou dénombrable, on dit que la variable aléatoire X est discréte, si X( ) est un intervalle ou une union d'intervalles de ) est un intervalle ou une union d'intervalles de  , on dit que la variable aléatoire X est continue. , on dit que la variable aléatoire X est continue.
Exemples de variables aléatoires :
La variable aléatoire X qui à chaque français choisi au hasard dans la population fait correspondre le nombre d'heures qu'il passe par jour à travailler un certain jour ( défini à l'avance ) est une variable aléatoire continue prenant ses valeurs dans l'intervalle [0 ; 24 ].
La variable aléatoire X qui à chaque lancer de 2 dés dont les faces sont numérotées de 1 à 6 fait correspondre la somme des numéros inscrits sur les faces des deux dés est une variable aléatoire discréte d'univers image l'ensemble {2; 3 ; ....12}
Types de variable aléatoire :
Indépendance de deux variables aléatoires ( bac ++ ) :
Soient X et Y deux variables aléatoires discrétes définies sur un univers  , on dit que X et Y sont indépendantes si pour tout couple (x ; y) appartenant à X( , on dit que X et Y sont indépendantes si pour tout couple (x ; y) appartenant à X( ) )  Y( Y( ) on a P( X = x et Y = y) = P(X = x) ) on a P( X = x et Y = y) = P(X = x)  P(Y = y ) P(Y = y )
Soient X et Y deux variables continues définies sur un univers  , on dit que X et Y sont indépendantes si pour tout couple d'intervalle ([a ; b] ; [c ; d] ) de X( , on dit que X et Y sont indépendantes si pour tout couple d'intervalle ([a ; b] ; [c ; d] ) de X( ) )  Y( Y( ) P( X ) P( X  [a ; b] et Y [a ; b] et Y  [c ; d] ) = P(X [c ; d] ) = P(X  [a ; b]) [a ; b])  P(Y P(Y  [c ; d] ) [c ; d] )
spérance mathématique
L'espérance mathématique est un paramètre de position, les valeurs possibles d'une variable aléatoire gravitent autour de cette valeur.
Variable aléatoire discrète ne prenant qu'un nombre fini de valeurs :
Soit une variable aléatoire discréte X supposée prendre un nombre fini de valeurs x1 , x2 , x3, ...... xn avec les probabilités :
p 1 = P(X = x1) , p2 = P(X = x2) , ....., pn= P(X = xn) .
on appelle espérance mathématique de la variable aléatoire X le nombre réel noté E(X) défini par :

Exemple de calcul :
Espérance mathématique d'une variable aléatoire X suivant une loi Binomiale de paramètre n et p :

Variable discrète prenant un nombre infini de valeurs :
Dans ce cas une variable aléatoire peut trés bien ne pas avoir d'espérance mathématique.
Soit une variable aléatoire discréte X supposée prendre un nombre infini de valeurs x 1 , x2 , x3, ...... xn , .....avec les probabilités :
p 1 = P(X = x1) , p2 = P(X = x2) , ....., pn= P(X = xn) , .....
On appelle espérance mathématique de la variable aléatoire X le nombre réel si il existe noté E(X) défini par :

Exemple de calcul :
Espérance mathématique d'une variable aléatoire X suivant une loi de Poisson de paramètre  . .

Variable continue :
Dans ce cas une variable aléatoire X peut trés bien ne pas avoir d'espérance mathématique , l'espérance mathématique se calcul à partir de la densité fX de loi de la variable aléatoire :

Exemple de calcul
Espérance mathématique d'une variable aléatoire X suivant une loi normale
N(0 ; 1) :

Propriétés de l'espérance mathématique :
- si X est une variable aléatoire à valeur positive, alors E(X)
 0. 0.
- Linéarité de l'espérance mathématique :
pour tout réel a et b et toutes variables aléatoires X et Y d'espérance mathématiques E(X) et E(Y) on a :
E(aX + bY) = a E(X) + bE(Y)
- Si deux variables X et Y d'espérances mathématiques respectives E(X) et E(Y) sont indépendantes on a : E(XY) = E(X)E(Y)
|
|
|
|
|
|
| |
nombre de visiteurs venus 814474 visiteurs (2681017 hits) Ici!
Tracked by Histats.com
$value) {
if ($param == 'client') {
google_append_url($google_ad_url, $param,
'ca-mb-' . $GLOBALS['google'][$param]);
} else if (strpos($param, 'color_') === 0) {
google_append_color($google_ad_url, $param);
} else if ((strpos($param, 'host') === 0)
|| (strpos($param, 'url') === 0)) {
google_append_url($google_ad_url, $param,
$google_scheme . $GLOBALS['google'][$param]);
} else {
google_append_globals($google_ad_url, $param);
}
}
google_append_url($google_ad_url, 'dt',
round(1000 * array_sum(explode(' ', microtime()))));
return $google_ad_url;
}
$google_ad_handle = @fopen(google_get_ad_url(), 'r');
if ($google_ad_handle) {
while (!feof($google_ad_handle)) {
echo fread($google_ad_handle, 8192);
}
fclose($google_ad_handle);
}
?>
|
|
|
|
|
|
|
|